CS 354 - Digital Systems Design (Section 02)
Spring-2024
Classes: MW 3:05pm - 4:20pm, Ebenezer D. Bassett Hall 311
Instructor: Dr. Zdravko Markov, 30307 Maria Sanford Hall, (860)-832-2711,
http://www.cs.ccsu.edu/~markov/,
e-mail: markovz at ccsu dot edu
Office hours: MW 4:30pm-6:00 pm, TR 10:45am-12:00pm, in person.
Book an appointment here.
Catalog data: An introduction to the analysis and design of digital systems in terms of logical and sequential networks. Various minimization techniques are studied.
Prerequisites: CS 254 and (MATH 217 or MATH 218)
Course Description: This course teaches how to design digital circuits at gate level. It includes theoretical material
on Boolean algebra and finite state machines, which are part of the fundamental
Computer Science theory. Students analyze and design combinational and
sequential circuits by using modern approaches to hardware simulation such
as the Hardware Description Language. They use hierarchical approaches
to create the basic components of the computer such as decoders, adders,
registers and memories. At the end, students use their knowledge to design
a simple central processing unit (CPU).
Course Learning Outcomes (CLO):
-
Understand the basics of Boolean algebra
-
Use minimization techniques to implement Boolean functions by logic gates
-
Implement basic combinational circuits as adders, multiplexers, encoders
and decoders
-
Understand the basics of synchronous sequential logic and finite state
machines
-
Implement clocked sequential circuits as registers, counters and memory
devices
-
Use a Hardware Description Language (HDL) to design and implement digital
circuits
-
Design and implement simple ALU and CPU
The CS 354 Course Learning Outcomes support the following Student
Outcomes (SO):
- SO-2: Design, implement, and evaluate a computing-based solution to meet a given set of computing requirements in the context of the program s discipline
(supported by CLO's 5, 6, 7).
- SO-6: Apply computer science theory and software development fundamentals to produce computing-based solutions
(supported by CLO's 1, 2, 3, 4).
Required textbook: Morris Mano & Michael Ciletti, Digital Design, 6th edition, Pearson, 2021.
Required software:
Class Participation: Regular attendance and
active class participation is expected from all students. If you must miss
a test, try to inform the instructor of this in advance. In case of missed
classes and work due to plausible reasons (such as illness or accidents)
limitted assistance will be offered. Unexcused absences will result in
the student being totally responsible for the make-up process.
Course Expectations for Out-of-Class Work:
To succeed in this 3-credit class, it is expected that you commit a total of 12 hours
per week to master the course material. This includes 2.5 hours of lecture time and
an additional 9.5 hours dedicated to independent study and coursework.
This time commitment aligns with the expectations set by the Computer Science
department for major courses and adheres to university policies.
Recognizing that dedicating this amount of time outside the classroom is a significant
commitment, it is nevertheless necessary for success. Please plan your course load
accordingly.
Assignments and tests: Reading and problem
assignments are listed below. Problems are to be done, but do not need
to be handed in. Some of the problems will be worked in class. There will
be three tests and a final exam. The tests will include questions
from the textbook, questions from the lectures, and questions from the
assigned projects.
Projects: There will be three projects
requiring the use of the Verilog Hardware Description Language to implement
and simulate digital circuits. The projects with their due dates are listed
below in the class schedule (the project descriptions will be available
in Blackboard). All projects must be submitted through the course
page in Blackboard at https://ccsu.blackboard.com/.
Grading: The final grade will be based on
projects (45%), tests (30%), and the final exam (25%), and will
be affected by classroom participation, conduct and attendance. All grades
will be availabe in Blackboard. The letter grades will be calculated
according to the following table:
| A |
A- |
B+ |
B |
B- |
C+ |
C |
C- |
D+ |
D |
D- |
F |
| 95-100 |
90-94 |
87-89 |
84-86 |
80-83 |
77-79 |
74-76 |
70-73 |
67-69 |
64-66 |
60-63 |
0-59 |
Unexcused late submission policy: Assignments
submitted more than two days after the due date will be graded one
letter grade down. Projects submitted more than a week late
will receive
two letter grades down. No submissions will
be accepted more than two weeks after the due date.
Honesty policy: The CCSU honor code for
Academic Integrity is in effect in this class. It is expected that all
students will conduct themselves in an honest manner and NEVER claim work
which is not their own. Violating this policy will result in a substantial
grade penalty, and may lead to expulsion from the University. You may find
it online at
http://web.ccsu.edu/academicintegrity/.
Please read it carefully.
Students with disabilities: Students who
believe they need course accommodations based on the impact of a disability,
medical condition, or emergency should contact me privately to discuss
their specific needs. I will need a copy of the accommodation letter from
Accessibility Services in order to arrange class accommodations. Contact
Office of Accessibility Services, Willard-DiLoreto Hall, Suite W201 if you are not already
registered with them. Office of Accessibility Services maintains the confidential
documentation of your disability and assists you in coordinating reasonable
accommodations with your faculty.
Tentative schedule of classes, assignments and tests
Note: Dates will be posted for all classes,
project and test due days (see also University
Calendar). Additional material may be posted too. Check the schedule
and the class pages regularly for updates!
- Jan 17:
Basic
components of the computer and its implementation: from instructions to
gates. Run the 4-bit CPU (download it from Blackboard
and use Digital
Works). Read Chapter 1.
- Jan 22:
Boolean algebra: basic definitions,
theorems and properties
- Jan 24:
Boolean functions
- Jan 29:
Canonical and standard form
of Boolean functions
- Jan 31:
Logic operations and
logic gates
- Feb 5:
Review of Chapter 2
- Feb 7: Test 1 (Chapter 2, max. grade: 10 pts)
- Feb 12:
Simplification of Boolean
functions: the map method
- Feb 14:
Four variable maps, don't-care conditions
- Feb 21:
NAND and NOR implementation of boolean
functions, other implementations of boolean functions
- Feb 26:
Review of Chapter 3. Problems: 3.1 - 3.13, 3.15 - 3.17, 3.18 - 3.23, 3.27
- 3.30.
- Feb 28:
Test 2 (Chapters 2 and 3, max. grade: 10 pts.)
- March 4:
Combinational logic: analysis, design, adders, subtractors, decimal adder
- March 6:
Basics of HDL and using Verilog, Project 1 posted
- March 18:
Verilog Lab: half-adder, full adder, incrementer using 4 half-adders, 4-bit adder.
- March 20:
Decoders, encoders and multiplexers
- March 25:
Read-only memory and PLA
- March 27:
Review of Combinational Logic, ROM, and PLA. Review Problems: 4.9, 4.10, 4.11, 4.23, 4.25,
4.27, 4.28, 4.31, 4.32, 4.33, 7.18, 7.19, 7.20, 7.28.
- March 27:
Project 1 due (max. grade: 15 pts.)
- April 1:
Test 3 (Chapter 4, ROM, and PLA, max. grade: 10 pts.). See Test 3 Practice Problems in Blackboard.
- April 3:
Using HDL to design combinational circuits
- April 8:
Designing an ALU. Project 2 posted
- April 10:
Synchronous sequential logic: flip-flops
- April 15:
Analysis of clocked sequential circuits: finite state
machines
- April 17:
Project 2 due (max. grade: 15 pts.)
- April 17:
Designing clocked sequential circuits
- April 22:
Designing a CPU, Project 3 posted
- April 24:
Register and counters
- April 29: Review of Synchronous Sequential Circuits
- April 30:
Extra credit Quiz (2-level NAND, decorder, ROM and PLA implementations, Synchronous Sequential Circuits). Online timed test (2 hours).
- May 1:
Project 3 due (max. grade: 15 pts.)
- May 1:
Review for Final Exam
- May 6, 1:00 PM - 3:00 PM
Final Exam (max. grade: 25 pts.) taken in class.
Boolean algebra: basic definitions, theorems
and properties
Reading: Book Sections 2.1 - 2.4
Exercises: Problems 2.1 - 2.3
Lecture Notes:
Axioms of Boolean algebra (set of elements B, two binary operators: + and
.):
-
Closure
-
Identity element
-
w.r.t. + denoted by 0: x+0=0+x=x
-
w.r.t. . denoted by 1: x.1=1.x=x
-
Commutative law
-
w.r.t. +: x+y=y+x
-
w.r.t. .: x.y=y.x
-
Distributive law
-
over +: x.(y+z)=(x.y)+(x.z)
-
over .: x+(y.z)=(x+y).(x+z)
-
Complement: for every x there exists x', such that:
-
There exist at least two distinct elements x, y in B.
Defining a boolean algebra:
-
Show the elements of B
-
Show the rules of the operators + and .
-
Show that the axioms are satisfied
-
Example of a Boolean Algebra: For any set A, the subsets of A form a Boolean
algebra under the operations of union, intersection and complement.
Binary logic (two-valued Boolean algebra):
-
B={0,1}
-
+ = OR, . = AND, ' = NOT (truth tables)
-
Closure
-
Identity: 0 for + and 1 for .
-
Commutative law: see the truth tables
-
Distributive law: show by a truth table
-
Complement: show by a truth table and by the complement table
-
There are two distinct elements in B: 0 and 1
Duality principle: interchange + and . operators and
replace 1's by 0's and 0's by 1's.
Basic theorems
-
x+x=x, x.x=x
-
x+1=1, x.0=0
-
(x')'=x (involution)
-
x+(y+z)=(x+y)+z, x.(y.z)=(x.y).z (associativity)
-
(x+y)'=x'.y', (x.y)'=x'+y' (DeMorgan's law)
-
x+xy=x, x.(x+y)=x (absorption)
Proofs by postulates and other theorems or by truth tables.
Boolean functions
Reading: Book Section 2.5
Exercises: Problems 2.4 - 2.9
Lecture Notes:
Defining Boolean functions
-
algebraic expression - infinite number of expressions for a single boolean
function.
-
truth table - unique representation.
Example 1: Boolean functions
F1 = xyz'
F2 = x + y'z
F3 = x'y'z + x'yz + xy'
F4 = xy' + x'z
| x y z |
F1 F2 F3 F4 |
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1 |
0 0 0 0
0 1 1 1
0 0 0 0
0 0 1 1
0 1 1 1
0 1 1 1
1 1 0 0
0 1 0 0 |
Implementing a Boolean function in Logic Gates (AND, OR, NOT)
-
Using the algebraic form:
-
literal: an input to a logic gate
-
term: logic gate
-
term and literal minimization
-
Using truth table - first transform into algebraic form, sum of products
Example 2: Building 1-bit adder
-
truth tables for result and carryout
-
transform into sum of products
-
build the logic diagram
Algebraic manipulations
-
minimization of literals
-
complement of a function, DeMorgan's theorem for more than two variables
(dual of the function and complement each literal):
-
(A+B+C+D+...)' = A'B'C'D'+...
-
(ABCD...)' = A'+B'+C'+D'+...
Example 3: Simplification (1<->2, 4<->5)
1. x+x'y = (x+x')(x+y) = 1(x+y) = x+y
2. x(x'+y) = xx'+xy = 0+xy = xy
3. x'y'z+x'yz+xy' = x'z(y'+y)+xy' = x'z+xy'
4. xy+x'z+yz = xy+x'z+yz(x+x') = xy+x'z+xyz+x'yz = xy(1+z)+x'z(1+y)
= xy+x'z
5. (x+y)(x'+z)(y+z) = (x+y)(x'+z)
Canonical and standard form of
Boolean functions
Reading: Book Section 2.6
Exercises: Problems 2.17 - 2.23, 2.30, 2.31
Lecture Notes:
1. Minterms and Maxterms
Minterms and maxterms for three variables
| x y z |
Minterms |
Maxterms |
| 0 0 0 |
x'y'z' m0 |
x + y + z M0 |
| 0 0 1 |
x'y'z m1 |
x + y + z' M1 |
| 0 1 0 |
x'yz' m2 |
x + y'+ z M2 |
| 0 1 1 |
x'yz
m3 |
x + y'+ z' M3 |
| 1 0 0 |
xy'z' m4 |
x'+ y + z M4 |
| 1 0 1 |
xy'z
m5 |
x'+ y + z' M5 |
| 1 1 0 |
xyz'
m6 |
x'+ y'+ z M6 |
| 1 1 1 |
xyz
m7 |
x'+ y'+ z' M7 |
2. Representing Boolean functions (truth table) by a sum of minterms
or by a product of maxterms
| x y z |
F F' |
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1 |
0 1
1 0
0 1
0 1
1 0
0 1
0 1
1 0 |
F = x'y'z + xy'z' + xyz = m1 + m4 + m7
F'= x'y'z' + x'yz' + x'yz + xy'z + xyz'
(F')' = F = (x+y+z)(x+y'+z)(x+y'+z')(x'+y+z')(x'+y'+z) = M0.M2.M3.M5.M6
Alternative notation: F = Sum(1,4,7), F = Prod(0,2,3,5,6)
3. Canonical form (sum of minterms or product of maxterms) of Boolean
functions
-
We have 2^(2^n) functions of n variables.
-
Transforming into sum of minterms:
-
From algebraic form directly (using distributive law and ANDing (x+x')
if x is missing).
-
Example: F = a + b'c = ... = Sum(1,4,5,6,7)
-
Using a truth table
-
Transforming into product of maxterms: using distributive law and ORing
xx'if
x
is missing).
-
Example: F = xy + x'z = ... = Prod(0,2,4,5)
4. Conversion between canonical forms
F=Sum(1,4,7)
F'=Sum(0,2,3,5,6)
F=(F')'=(Sum(0,2,3,5,6))'=Prod(0,2,3,5,6)
4. Standard form - sum of products or product of sums not necessarily
containing all variables in the individual terms
Logic operations and logic
gates
Reading: Book Section 2.7-2.8
Exercises: Problems 2.24 - 2.28
Lecture Notes:
1. The 16 Boolean functions of 2 variables (pdf)
2. Algebraic forms of the 16 functions of 2 variables (pdf)
3. Digital Logic gates and their implementation:
-
AND
-
OR
-
Inverter
-
Buffer
-
NAND
-
NOR
-
XOR
-
XNOR
4. Gates with multiple inputs and their implementation:
-
AND and OR: simple cascading
-
3-input NOR and NAND: not associative, change the definition to (x+y+z)'
and (xyz)'
-
Multiple input XOR and XNOR: associative, change the definition to "odd
number of 1's"
5. Implementing boolean functions with specific types of gates
- AND, OR, and NOT gates
- AND and NOT gates
- OR and NOT gates
- NAND gates
- NOR gates
Review of Chapter 2
Reading: Book Chapter 2
Exercises: Problems 2.1 - 2.9, 2.14, 2.15, 2.17 - 2.28, 2.30, 2.31
Lecture Notes:
-
Boolean algebra: basic definitions, theorems and properties
-
Boolean functions. Algebraic simplification
-
Canonical and standard form of Boolean functions.
-
Logic operations and logic gates
-
Implementation of the Boolean functions in logic gates:
-
Example 1. Function F is defined by the following truth table:
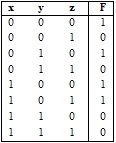
- Obtain the boolean expressions of F as a sum of minterms and a product of maxterms
-
Simplify both forms of F to minimal number of terms
- Implement the simplified function by using:
- AND, OR, and NOT gates
- AND and NOT gates
- OR and NOT gates
- NAND gates
- Example 2:
- Show the boolean function implemented in the follwing diagram.
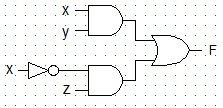
- Obtain the canonical form of the function as a sum of minterms by algebraic transformations.
- Obtain the canonical form of the function as a product of maxtermss by algebraic transformations.
Simplification of Boolean
functions - the map method
Reading: Book Sections 3.1, 3.2, 3.4
Exercises: Problems 3.1 - 3.3
Maps
Lecture Notes:
1. Map representation of Boolean functions
Two-variable map (properties)
| x \ y |
0 |
1 |
| 0 |
x'y' |
x'y |
| 1 |
xy' |
xy |
Examples:
xy
x+y = x(y+y')+y(x+x') = xy+xy'+yx+yx' = xy+xy'+yx'
(x+y)' = x'y'
Three-variable map (note the sequence)
| x \ yz |
00 |
01 |
11 |
10 |
| 0 |
x'y'z' |
x'y'z |
x'yz |
x'yz' |
| 1 |
xy'z' |
xy'z |
xyz |
xyz' |
Example: a + b'c = ... = Sum(1,4,5,6,7)
2. Simplification using maps (minimization of the number of terms)
3-variable map
-
Adjacent squares (including m0 and m2, m4 and m6). Example: Sum(3,4,6,7)
= xz'+yz
-
1 square - a term with 3 literals
-
2 adjacent squares - a term with 2 literals
-
4 adjacent squares - a term with 1 literal
-
8 adjacent squares - constant function 1
-
Using adjacent squares more than once. Example: Sum(0,2,4,5,6) = z'+xy'
-
Using a standard form (sum of product) - representing a product as adjacent
squares. Example: x'z+x'y+xy'z+yz
(mapping)
3. Product of sum simplification
(maxterm map)
x'y+x'y' = m0+m1 = x' = M2.M3 = x'
Example: F(x,y,z) = Sum(0,1,2,5)
Four variable maps, don't-care conditions
Reading: Book Section 3.3, 3.5
Exercises: Problems 3.4 - 3.13
Maps
Lecture Notes:
1. Four-variable map
(mapping)
| m0 |
m1 |
m3 |
m2 |
| m4 |
m5 |
m7 |
m6 |
| m12 |
m13 |
m15 |
m14 |
| m8 |
m9 |
m11 |
m10 |
| wx\yz |
00 |
01 |
11 |
10 |
| 00 |
w'x'y'z' |
w'x'y'z |
w'x'yz |
w'x'yz' |
| 01 |
w'xy'z' |
w'xy'z |
w'xyz |
w'xyz' |
| 11 |
wxy'z' |
wxy'z |
wxyz |
wxyz' |
| 10 |
wx'y'z' |
wx'y'z |
wx'yz |
wx'yz' |
Example 1: Sum(0,1,2,4,5,6,8,9,12,13,14) = y'+w'z'+xz'
| wx\yz |
00 |
01 |
11 |
10 |
| 00 |
1 |
1 |
|
1 |
| 01 |
1 |
1 |
|
1 |
| 11 |
1 |
1 |
|
1 |
| 10 |
1 |
1 |
|
|
Example 2: Sum(0,1,2,6,8,9,10) = x'y'+x'z'+w'yz'
| wx\yz |
00 |
01 |
11 |
10 |
| 00 |
1 |
1 |
|
1 |
| 01 |
|
|
|
1 |
| 11 |
|
|
|
|
| 10 |
1 |
1 |
|
1 |
2. A systematic approach to combining adjacent squares - prime implicants
(max number of squares)
Example 3: Sum(0,2,3,5,7,8,9,10,11,13,15)
| wx\yz |
00 |
01 |
11 |
10 |
| 00 |
1 |
|
1 |
1 |
| 01 |
|
1 |
1 |
|
| 11 |
|
1 |
1 |
|
| 10 |
1 |
1 |
1 |
1 |
-
Essential prime implicant for m5, m7, m13, m15: xz
-
Essential prime implicant for m0, m2, m8, m10: x'z'
-
Prime implicants for m3, m9, m11: yz, x'y, wz, wx'
3. Incompletely specified functions (don't-care conditions)
Example: F(a,b,c,d) = Sum(1,3,7,11,15), D(a,b,c,d) = Sum(0,2,5)
4. The tabulation method (optional)
4.1. Determination of prime implicants
Example 1: F = Sum(0,1,2,8,10,11,14,15)
| w x y z |
w x y z |
w x y z |
0 0 0 0 0 *
---------------
1 0 0 0 1 *
2 0 0 1 0 *
8 1 0 0 0 *
---------------
10 1 0 1 0 *
---------------
11 1 0 1 1 *
14 1 1 1 0 *
---------------
15 1 1 1 1 * |
0,1 0 0 0 -
0,2 0 0 - 0 *
0,8 - 0 0 0 *
------------------
2,10 - 0 1 0 *
8,10 1 0 - 0 *
------------------
10,11 1 0 1 - *
10,14 1 - 1 0 *
------------------
11,15 1 - 1 1 *
14,15 1 1 1 - * |
0,2,8,10 - 0 - 0
0,8,2,10 - 0 - 0
----------------------
10,11,14,15 1 - 1 -
10,14,11,15 1 - 1 -
|
F = w'x'y' + x'y' + wy
-
Compare to the map method (same implicants)
-
Decimal comparison (difference by a power of 2)
-
Example 2: F = Sum(1,4,6,7,8,9,10,11,15)
-
Tabulation: F=x'y'z + w'xz' + w'xy + xyz + wyz + wx'
-
Map: F=x'y'z + w'xz' + xyz + wx'
4.2. Selection of prime implicants
1 4 6 7 8 9 10 11 15
x'y'z 1,9
x
x
w'xz' 4,6
x x
w'xy 6,7
x x
xyz 7,15
x
x
wyz 11,15
x x
wx' 8,9,10,11
x x x x |
-
Include all essential prime implicants (covering a single term):
(1,9), (4,6), (8,9,10,11)
-
Choose minimal number of prime implicants: (7,15)
NAND and NOR implementation of boolean functions,
other implementations of boolean functions
Reading: Book Sections 3.6 - 3.8
Exercises: Problems 3.15 - 3.18, 3.19 - 3.23, 3.27 - 3.30
Lecture Notes:
-
Useful graphic symbols:
-
NAND or Invert-OR
-
NOR or Invert-AND
-
NAND-NAND (two level) implementation of Boolean functions. Example: F=xy+x'y'z'+x'yz'
-
Simplify the function (sum of products)
-
A NAND gate for each term (first level)
-
A single NAND gate at the second level with inputs coming from the outputs
of the first level NAND's
-
NOR-NOR implementation - the dual of the NAND-NAND
-
Example: F=xy+x'y'z'+x'yz'. Implement F
and F' by NAND-NAND, NOR-NOR and inverted the output.
-
Multilevel NAND implementation. Example: F=(AB'+A'B)(C+D')
-
Create an AND-OR multilevel implementation
-
Convert AND gates into NAND gates by inserting bubbles along the output.
-
Convert OR gates into NAND gates (inserting bubbles at the inputs
if necessary)
-
Remove all pairs of bubbles along the same line.
-
Replace the remaining bubles with one-input NAND gates
-
Multilevel NOR implementation. Example: F=(AB'+A'B)(C+D')
-
Nondegenerate forms of two level implementations:
-
AND-OR, OR-AND
-
NAND-NAND
-
NOR-NOR
-
NAND-AND, AND-NOR (AND-OR-INVERT)
-
OR-NAND, NOR-OR (OR-AND-INVERT)
-
XOR function (difference)
-
Properties
-
AND-OR-NOT implementation
-
NAND implementation
-
Odd function
-
XOR with more than two inputs
-
implementation by cascading XOR's
-
Parity checking
Basics of HDL and using Verilog and Digital
Works
Reading: Book Section 3.9, Section 4.12
Exercises: Problems 3.31, 3.32, 3.34 - 3.37
Lecture Notes:
Digital Works
Verilog HDL
-
Modules
-
Gate-level description
-
Test bench simulation
-
Example: implement a 3-input XOR, F(A,B,C) = A XOR B XOR C
// HDL Example (hierarchical design)
//----------------------------------
module my_xor(A,B,C);
input A,B;
output C;
wire x,y,z;
nand g1 (x,A,B),
g2 (y,A,x),
g3 (z,x,B),
g4 (C,y,z);
endmodule
module my_xor3(A,B,C,D);
input A,B,C;
output D;
wire x;
my_xor XOR1 (A,B,x),
XOR2
(x,C,D);
endmodule
module test_xor3;
reg A,B,C; // reg for inputs
wire D; // wire for outputs
my_xor3 xor3(A,B,C,D); // Instantiate my_xor3
initial
begin
$monitor("%1d %b %b %b %b",$time,A,B,C,D);
$display(" A B C D");
A=0;
B=0; C=0;
#1 A=0; B=0; C=1;
#1 A=0; B=1; C=0;
#1 A=0; B=1; C=1;
#1 A=1; B=0; C=0;
#1 A=1; B=0; C=1;
#1 A=1; B=1; C=0;
#1 A=1; B=1; C=1;
end
endmodule
-
Icarus Verilog (http://bleyer.org/icarus/).
-
Note about installation: use the latest stable release (iverilog-0.9.7_setup.exe)
and don't use folder names that include spaces, like Program Files.
- Online compiler:
https://www.jdoodle.com/execute-verilog-online
-
Write the Verilog source file: 4-bit-adder.vl
-
Compile:
C:\CS354\HDL>iverilog 4-bit-adder.vl
-
Run:
C:\CS354\HDL>vvp a.out
0000 0000 0 0000 0
0
0000 0001 1 0010 0
10
0001 0111 1 1001 0
20
1111 0000 1 0000 1
30
Combinational logic: analysis, design, adders, subtractors, decimal adder
Reading: Book Sections 4.1 - 4.6
Exercises: Problems: 4.6, 4.9, 4.10, 4.11.
Slides: Chapter
4 figures
Lecture Notes:
-
Two types of logic circuits:
-
Combinational logic (set of m Boolean functions of n variables),
example: 7-segment LED display.
-
Sequential (output are determined not only by the inputs, but also by internal
states).
-
Analysis of digital circuits:
-
Combinational or sequential? (no memory elements, no feedback)
-
Determine the Boolean function
-
Design procedure
-
Determine the number of inputs and outputs
-
Derive the truth table
-
Simplify the boolean function
-
Draw the logic diagram
-
Code conversion example: 3-bit 2's complementer
-
Adders: 0+0=0, 0+1=1, 1+0=1, 1+1=10.
-
1-bit half-adder: add two bits (x, y) and produce sum (S)
and carry (C).
-
Separate circuit implementation: C=xy, S=xy'+x'y (XOR).
-
Sharing components implementations: C=xy, S=(C+x'y')'; C=(x'+y')',
S=(x+y)(x'+y').
-
1-bit full-adder: add two bits and the carry from previous digit (x,
y, z) and produce sum (S) and carry (C).
-
Direct implementation: truth table, sum of minterms (C=xy+xz+yz, S=x'y'z+x'yz'+xy'z'+xyz).
-
Cascading two half adders: S = add(add(x,y),z), C = C1+C2.
-
Hierarchical design: 4-bit adder by cascading 4 1-bit adders.
-
Subtractors: 0-0=0(B=0), 0-1=1(B=1), 1-0=1(B=0), 1-1=0(B=0).
-
Half-subtractor: subtract two bits and produce result and borrow.
-
Full-subtractor: subtract two bits taking into account a borrow from the
previous digit.
-
N-bit binary adder
-
direct implementation: truth table with 2^(n+1) rows
-
hierarchical implementation: cascading n 1-bit adders (serial, parallel)
-
Adder-subtractor (two's complement numbers)
-
Carry propagation (delay) and carry look-ahead logic
-
carry propagate: Pi = Ai
xor Bi
-
carry generate: Gi = Ai.Bi
-
carry look-ahead logic: Ci+1 = Gi
+ Pi.Ci
-
4-bit adder with carry look-ahead: 4 half adders (xor, and) + carry look-ahead
+ 4 xor's
-
Detecting overflow:
-
Overflow(A3, B3, S3)
-
Overflow(C3,C4) = C3 XOR C4.
-
BCD adder: 4-bit adder + correction logic (if sum>1010 then add
0110
and produce decimal carry)
Decoders, encoders and multiplexers
Reading: Book Section 4.9 - 4.11
Exercises: Problems: 4-23, 4-25, 4-27, 4-28, 4-31, 4-32, 4.33
Slides: Chapter
4 figures
Lecture Notes:
1. Decoders (n to 2^n) - minterm implementation (AND gates)
| x y z |
D0 D1 D2 D3 D4 D5 D6
D7 |
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1 |
1 0 0 0 0
0 0 0
0 1 0 0 0
0 0 0
0 0 1 0 0
0 0 0
0 0 0 1 0
0 0 0
0 0 0 0 1
0 0 0
0 0 0 0 0
1 0 0
0 0 0 0 0
0 1 0
0 0 0 0 0
0 0 1 |
2. NAND implementation: inverted outputs and enable (E) input
| E x y |
D0 D1 D2 D3 |
1 X X
0 0 0
0 0 1
0 1 0
0 1 1 |
1 1 1 1
0 1 1 1
1 0 1 1
1 1 0 1
1 1 1 0 |
3. Decoders/Demultiplexers
4. Cascading decoders by using the E input (4 X 16 made by two 3
X 8)
5. Implementing combinational circuits using decoders:
-
the decoder outputs generate the minterms
-
add an OR gate to produce the sum
-
Example: full adder S(x,y,z)=Sum(1,2,4,7); C(x,y,z)=Sum(3,5,6,7)
5. Encoders (OR gates)
| D0 D1 D2 D3 |
x y |
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1 |
0 0
0 1
1 0
1 1 |
6. Ambiguities: undefined inputs (more than one set to 1), D0
is a don't care input. Solution: priority encoder
| D0 D1 D2 D3 |
x y V |
0 0 0 0
1 0 0 0
X 1 0 0
X X 1 0
X X X 1 |
X X 0
0 0 1
0 1 1
1 0 1
1 1 1 |
Map: x=D2+D3,
y=D1.D2'+D3
,
V=D0+D1+D2+D3
7. Multiplexers (decoder + 1 input for each AND + second level OR)
| s1 s0 |
Output |
0 0
0 1
1 0
1 1 |
I0
I1
I2
I3 |
8. Implementing Boolean functions with a multiplexer: assigning
functional value to each input (each combination of select lines)
9. Three-state gates. Implementing multiplexers with three-state
gates: using a decoder for the three-state control inputs
Designing an ALU
Slides: MIPS ALU
Reading: Patterson, Hennessy: Computer Organization and Design,
4th Edition: Appendix
C.5 - Constructing a Basic Arithmetic Logic Unit
Programs: ALU4-behavioral.vl
Lecture Notes:
-
The datapath and the ALU
-
ALU operations
-
arithmetic and logic (add, sub, and, or)
-
set on less than (slt)
-
Implementing subtraction:
-
A+B = A+(-B)
-
negation in two's complement: invert and add 1
-
Cascading 32 1-bit ALU's
-
Implementing subtraction - negation in two's complement: invert and add
1
-
Invert (multiplexer or XOR)
-
Add 1 - set the first carry to 1
-
Implementing slt: add Set and Less lines
-
Test for equality and completing the ALU
Using HDL to design combinational circuits
Reading: Book Section 4.12
Exercises: run the verilog programs shown below
Lecture Notes:
1. Gate-Level Modeling
-
Example: 2x4 decoder
module decoder_gl (A,B,E,D);
input A,B,E;
output [0:3]D;
wire Anot,Bnot,Enot;
not
n1 (Anot,A),
n2 (Bnot,B),
n3 (Enot,E);
nand
n4 (D[0],Anot,Bnot,Enot),
n5 (D[1],Anot,B,Enot),
n6 (D[2],A,Bnot,Enot),
n7 (D[3],A,B,Enot);
endmodule
-
Example: 4-bit adder
// Description of half adder (see Fig 4-5b)
module halfadder (S,C,x,y);
input x,y;
output S,C;
//Instantiate primitive gates
xor (S,x,y);
and (C,x,y);
endmodule
//Description of full adder (see Fig 4-8)
module fulladder (S,C,x,y,z);
input x,y,z;
output S,C;
wire S1,D1,D2; //Outputs of first XOR and two AND
gates
//Instantiate the halfadder
halfadder HA1 (S1,D1,x,y),
HA2 (S,D2,S1,z);
or g1(C,D2,D1);
endmodule
//Description of 4-bit adder (see Fig 4-9)
module _4bit_adder (S,C4,A,B,C0);
input [3:0] A,B;
input C0;
output [3:0] S;
output C4;
wire C1,C2,C3; //Intermediate carries
//Instantiate the fulladder
fulladder FA0 (S[0],C1,A[0],B[0],C0),
FA1 (S[1],C2,A[1],B[1],C1),
FA2 (S[2],C3,A[2],B[2],C2),
FA3 (S[3],C4,A[3],B[3],C3);
endmodule
2. Dataflow Modeling
-
Example: 2x4 decoder
// Dataflow description of a 2-to-4-line decoder
module decoder_df (A,B,E,D);
input A,B,E;
output [0:3] D;
assign D[0] = ~(~A && ~B && ~E),
D[1] = ~(~A
&& B && ~E),
D[2] = ~(A
&& ~B && ~E),
D[3] = ~(A
&& B && ~E);
endmodule
-
Example: 4-bit adder
// Dataflow description of 4-bit adder
module binary_adder (A,B,Cin,SUM,Cout);
input [3:0] A,B;
input Cin;
output [3:0] SUM;
output Cout;
assign {Cout,SUM} = A + B + Cin;
endmodule
3. Behavioral Modeling
//Behavioral description of 2-to-1-line multiplexer
module mux2x1_bh(A,B,select,OUT);
input A,B,select;
output OUT;
reg OUT;
always @ (select or A or B)
if (select ==
1) OUT = A;
else OUT = B;
endmodule
//Behavioral description of 4-to-1- line multiplexer
//Describes the function table of Fig. 4-25(b).
module mux4x1_bh (i0,i1,i2,i3,select,y);
input i0,i1,i2,i3;
input [1:0] select;
output y;
reg y;
always @ (i0 or i1 or i2 or i3 or select)
case (select)
2'b00: y = i0;
2'b01: y = i1;
2'b10: y = i2;
2'b11: y = i3;
endcase
endmodule
4. Simulation by using test bench
//Stimulus for mux2x1_df.
module testmux;
reg TA,TB,TS; //inputs for mux
wire Y; //output from
mux
mux2x1_df mx (TA,TB,TS,Y); // instantiate mux
initial
begin
TS = 1; TA = 0; TB = 1;
#10 TA =
1; TB = 0;
#10 TS =
0;
#10 TA =
0; TB = 1;
end
initial
$monitor("select = %b A = %b B =
%b OUT = %b time = %0d",
TS, TA, TB, Y, $time);
endmodule
//Dataflow description of 2-to-1-line multiplexer
//from Example 4-6
module mux2x1_df (A,B,select,OUT);
input A,B,select;
output OUT;
assign OUT = select ? A : B;
endmodule
Read-only memory and PLA
Reading: Book Sections 7.5, 7.6
Exercises: Problems: 7.17, 7.18, 7.19, 7.20
Slides: Chapter
7 figures
Lecture Notes:
-
Implementing Boolean functions by using "programmable" decoders: minterms
(decoder outputs) + OR gate (F). Array logic notation.
-
Read-only memory (ROM): (address space) X (word size), i.e.
2^n X m - sum of minterms
-
Combinational logic implementation: decoder + fuses + OR gates (for each
bit in the word), array logic notation for OR gates.
-
Types of ROM: PROM, EPROM
-
Programmable logic array (PLA) - sum of products. Example: F1(A,B,C)=SUM(3,4,5,7), F2(A,B,C)=SUM(3,5,7)
-
Simplify the functions for each output bit (using maps), F1=AB'+BC, F2=AC+BC
-
Create a table with as many rows as the total number of products: 3 rows
(AB', BC, AC)
-
First column: product terms; second column: inputs; third column: outputs
-
Draw the diagram using array logic notation
- Example 1: MIPS CPU control
-
Example 2:
-
F1(A,B,C)=SUM(0,1,2,4)
-
F2(A,B,C)=SUM(0,5,6,7)
-
Sum of product maps:
-
F1 = A'B'+ A'C'+ B'C'
-
F1'= AB + AC + BC
-
F2 = AB + AC + A'B'C'
-
F2'= A'C+ A'B + AB'C'
-
Products: AB, AC, BC, A'B'C'
-
Example 3: PLA for BCD-to-seven-segment decoder (Problem 4.9).
Synchronous sequential logic: flip-flops
Reading: Book Sections 5.1 - 5.4
Exercises: Problems: 5.6 - 5.10
Slides: Chapter
5 figures
Lecture Notes:
-
Combinational and sequential logic
-
Synchronous and asynchronous logic:
-
Synchronous: behavior is determined by the inputs signals at discrete instants
of time (clock pulses), clocked sequential circuits.
-
Asynchronous: behavior is determined by the signals at any instant of time
and the order in which the inputs change.
-
Memory elements (binary storage): flip-flops
-
Basic flip-flops (operate with signal level).
-
SR latch
-
D latch: SR latch with control (enable input)
-
Edge-Triggered flip-flops:
-
respond to clock pulse edges: positive and negative
-
master-slave D flip-flop: samples the input during the high clock pusle
level, changes the state (Q) at negative edge.
-
JK and T flip-flops
-
JK flip-flop - changes the state at the clock pulse edge, implemented with
a D flip-flop: D=JQ'+K'Q
-
T flip-flop - complements its state:
-
implemented with JK flip-flop: T=J=K (T=1 changes the state).
-
implemented with D flip-flop: D = TQ' + T'Q = T XOR Q
- HDL implementations (T-flip-flop.vl)
module D_flip_flop(D,CLK,Q);
input D,CLK;
output Q;
wire CLK1, Y;
not not1 (CLK1,CLK);
D_latch D1(D,CLK, Y),
D2(Y,CLK1,Q);
endmodule
module D_latch(D,C,Q);
input D,C;
output Q;
wire x,y,D1,Q1;
nand nand1 (x,D, C),
nand2 (y,D1,C),
nand3 (Q,x,Q1),
nand4 (Q1,y,Q);
not not1 (D1,D);
endmodule
module test_D_flip_flop;
reg D,C;
wire Q;
D_flip_flop D1(D,C,Q);
initial
begin
D=0;
C=0;
#10 D=0; C=1;
#10 D=0; C=0;
#10 D=1; C=0;
#10 D=1; C=1;
#10 D=0; C=1;
end
initial
$monitor("%d %b %b %b",$time,D,C,Q);
endmodule
Designing a CPU
Lecture Notes:
- Simple MIPS program
li $t1, 7 # $t1 = 7
li $t2, 5 # $t2 = 5 (4'b0101)
sub $t3, $t1, $t2 # $t3 = 2 (7-5=2)
li $t3, 10 # $t3 = 10 (4'b1010)
or $t2, $t2, $t3 # $t2 = 15 (4'b1111)
and $t3, $t2, $t3 # $t3 = 10 (4'b1010)
slt $t2, $t3, $t2 # $t2 = 1
add $t2, $t3, $t2 # $t2 = 11 (4'b1011=-5)
add $t3, $t1, $t2 # $t3 = 2 (7+(-5)=2)
slt $t1, $t2, $t3 # $t1 = 0
-
Instruction set architecture (instuction format)
-
Instruction register (D flip-flop register)
-
Register file (diagram)
-
CPU datapath and control (diagram)
-
HDL behavioral implementation (4-bitCPU.vl)
Analysis of clocked sequential circuits: finite
state machines
Reading: Book Section 5.5
Exercises: Problems: 5.6 - 5.10
Slides: Chapter
5 figures
Lecture Notes:
1. Characteristic tables and equations: describing logical properties of
a flip-flop. Using time for indexing the state output.
-
RS flip-flop: Q(t+1)=SQ'(t)+R'Q(t)
| S R |
Q(t+1) |
0 0
0 1
1 0
1 1 |
Q(t)
0
1
? |
-
JK flip-flop: Q(t+1)=JQ'(t)+K'Q(t)
| J K |
Q(t+1) |
0 0
0 1
1 0
1 1 |
Q(t)
0
1
Q'(t) |
-
T flip-flop: Q(t+1)=TQ'(t)+T'Q(t)
2. Sequential circuit examples (Seq-Circuit-D, Seq-Circuit-T, Seq-Circuit-T1, Figures 5.15- 5.20)
- Logic diagram (D flip-flops)
DA = xA'B + xAB'
DB = xB'
y = AB
-
State table: <present state> X <input> -> <next state>; <present
state> -> <output>
Present state
A B |
Input
x |
Next state
A B |
Output
y |
0 0
0 0
0 1
0 1
1 0
1 0
1 1
1 1 |
0
1
0
1
0
1
0
1 |
0 0
0 1
0 0
1 0
0 0
1 1
0 0
0 0 |
0
0
0
0
0
0
1
1 |
- State diagram - finite state machines
-
Mealy model: <present state> X <input> -> <output> (output
may change during the pulse)
-
Moore model: <present state> -> <output>
3. Finite State Machines
Designing clocked sequential circuits
Reading: Book Section 5.8
Exercises: Problems: 5-16, 5-19, 5-20.
Slides: Chapter
5 figures
Lecture Notes:
Flip-flop excitation tables
-
D flip-flop
| Q(t) Q(t+1) |
D |
0 0
0 1
1 0
1 1 |
0
1
0
1 |
-
T flip-flop
| Q(t) Q(t+1) |
T |
0 0
0 1
1 0
1 1 |
0
1
1
0 |
Designing a sequential curcuit
Example: if x=1 count 0,1,2,3,0,1,2,3,... ; if x=0 no change; output
y=1 if state=3 and x=1, else y=0.
1. Description of the circuit behavior: number of states, inputs, outputs,
functionality.
2. State diagram (number of states -> number of flip-flops)
3. State table
Present state
A B |
Input
x |
Next state
A B |
Output
y |
0 0
0 0
0 1
0 1
1 0
1 0
1 1
1 1 |
0
1
0
1
0
1
0
1 |
0 0
0 1
0 1
1 0
1 0
1 1
1 1
0 0 |
0
0
0
0
0
0
0
1 |
4. Excitation table (D flip-flops)
Present state
A B |
Input
x |
Next state
A B |
Flip-flop inputs
DA DB |
0 0
0 0
0 1
0 1
1 0
1 0
1 1
1 1 |
0
1
0
1
0
1
0
1 |
0 0
0 1
0 1
1 0
1 0
1 1
1 1
0 0 |
0 0
0 1
0 1
1 0
1 0
1 1
1 1
0 0 |
5. Excitation table (T flip-flops)
Present state
A B |
Input
x |
Next state
A B |
Flip-flop inputs
TA TB |
0 0
0 0
0 1
0 1
1 0
1 0
1 1
1 1 |
0
1
0
1
0
1
0
1 |
0 0
0 1
0 1
1 0
1 0
1 1
1 1
0 0 |
0 0
0 1
0 0
1 1
0 0
0 1
0 0
1 1 |
6. Block diagram: two flip-flops (D or T) + combinational circuit
7. Designing the combinational circuit (maps)
-
D flip-flops:
-
DA = xA'B + x'A + AB'
-
DB = x'B + xB'
-
T flip-flops:
8. Counters: changing the state at each clock pulse, state bits as outputs,
no inputs. Example: three-bit counter with T flip-flops.
Register and counters
Reading: Book Sections 6.1 - 6.4
Exercises: Problems: 6.3, 6.4, 6.6, 6.17, 6.19, 6.27, 6.28.
Slides: Chapter
6 figures
Lecture Notes:
-
Registers: a group of binary cells (flip-flops) suitable for storing binary
information
-
Gated latch: accepting inputs during the clock pulse (C=1). Example: a
group of D flip flops (Fig.6-1)
-
Loading registers
-
Parallel loading: providing access to all inputs at a time.
-
C controlled loading (C acts as an enable signal)
-
Load control input
-
applied to C. Example: D flip-flops with their C input anded with the load
control input (delay of C).
-
applied to all data inputs. Register with D flip-flops: load control used
to switch between previous state and input (Fig. 6-2).
-
Building sequential circuits with registers: equivalent to the D flip-flop
implementation of sequential circuits with load control=1.
-
Shift registers: using edge triggered D flip-flops, serial input, serial
output (Fig.6-3), shift control, serial transfer (Fig.6-4)
-
Serial addition (Fig. 6-5).
-
Counters
-
Synchronous counters (C applied to all flip-flops): flip-flops + combinational
logic (see "Designing clocked sequential circuits")
-
Ripple counters: series of complementing flip-flops with the output of
each flip-flop connected to the C input of the next one.
-
Binary ripple counter: T flip-flops or D flip-flops (Fig.6-8).
-
BCD ripple counter: state diagram (Fig. 6-9), logic diagram (Fig.6-10).
Sample problems for Test 2 (Chapters 2 and 3)
Problem 1: Simplify F algebraically to the indicated number
of terms:
-
F = A'C' + ABC + AC' to a sum of two terms
-
F = (x'y'+ z)'+ z + xy + wz to a sum of three variables
-
F = A'B(D'+ C'D) + B(A + A'CD) to one variable
Problem 2: Find the complement of an expression
- see Problems 2.8, 2.20.
Problem 3: Transform F into canonical form as a sum
of minterms using a map.
-
F = (xy + z)(y + xz)
-
F = (A'+ B)(B + C')
Problem 4: Transform F into canonical
form as a sum of minterms algebraically.
-
F = (xy + z)(y + xz)
-
F = (A'+ B)(B + C')
Problem 5: Transform F into canonical form as a product
of maxterms (algebraically or by using a map).
-
F = (xy + z)(y + xz)
(map)
-
F = (A'+ B)(B + C')
Problem 6: Simplify the function algebraically to a sum
of three terms and implement the simplified function in standard
logic (using AND, OR and NOT gates).
F = xy'z + x'y'z + w'xy + wx'y + wxy
Problem 7: Using the map method simplify
in sum of products the following functions. Show which map squares
are covered by which term from the original function.
-
F = x'z'+ y'z'+ yz'+ xy
-
F = (A'+ B'+ D')(A + B'+ C')(A'+ B + D')(B + C'+ D')
Problem 8: Using the map method simplify
in product of sums the following functions. Show which map squares
are covered by which term from the original function.
-
F = x'z'+ y'z'+ yz'+ xy
-
F = (A'+ B'+ D')(A + B'+ C')(A'+ B + D')(B + C'+ D')
Problem 9: Implement the simplified
functions from Problems 7 and 8 using two-level NAND logic
Problem 10: Implement the simplified
functions from Problems 7 and 8 using two-level NOR logic
Problem 11: Implement in two-level NOR
logic the function F(w,x,y,z)=SUM(0,1,2,3,4,8,9,12)
Problem 12: Implement in two-level NAND logic
the function F(x,y,z)=PROD(2,4)
Review for Final Exam
- See Final Exam Review Questions in Blackboard
- Practice Problems
-
Combinational circuits (Chapter 4). Problems: 4.9, 4.10, 4.11, 4.23, 4.25,
4.27, 4.28, 4.31, 4.32, 4.33
-
ROM and PLA (Chapter 7). Problems 7.17, 7.18, 7.19, 7.20.
-
Clocked sequential circuits (Chapter 5). Problems: 5.6 - 5.10, 5.16, 5.19,
5-20.
Project 1 (15 pts.)
Building and testing basic combinational circuits by using Verilog HDL
Log on to Blackboard
Learn to see and submit the project.
Project 2 (15 pts.)
Building a 4-bit ALU
Log on to Blackboard
Learn to see and submit the project.
Project 3 (15 pts.)
Building a 4-bit CPU
Log on to Blackboard
Learn to see and submit the project.